In this article you will be given a tutorial on syllogistic reasoning – a type of deductive reasoning. You will learn about:

• The relationship between syllogistic reasoning and IQ.
• What is syllogistic reasoning.
• Mindware strategy tips on how to use diagrams and rules to improve your syllogistic reasoning.

Syllogistic reasoning and IQ

A study in this the March 2011 issue of Intelligence has demonstrated with a large Japanese twin sample  “a close association between syllogistic reasoning ability and general intelligence” (Article reference here). Syllogistic reasoning is an important type of deductive reasoning, and deductive reasoning is a key to your IQ.

According to our strategy-capacity training method, training deductive reasoning is an effective method for helping increase IQ.

What is syllogistic reasoning and what is a syllogism?

Aristotle’s Syllogisms

Here is an example of a syllogism:

Syllogism 1

All humans are animals.
All animals are mortal.
Therefore, all humans are mortal.

A syllogism is a type of logical argument in which a pair of sentences serve as the premises and a third sentence serves as the conclusion. The example above is a valid syllogism. What makes it valid is that if the premises are true, then it follows necessarily that the conclusion is also true.

We can see how deductive arguments are valid by drawing circles. For Syllogism 1, let circle ‘H’ represent the set of all humans,  circle ‘A’ represent the set of all animals, and circle ‘M’ represent the set of all mortal things. The first premise says the set of all men is contained in the set of all mortal things – so we can put circle H inside circle A to represent what would be needed for the first premise to be true.

 

Adding the second premise we get:

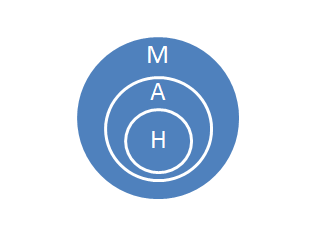
You can see from the diagram that necessarily H is inside M – which is what the conclusion asserts.

What makes a syllogism valid is that in any way you represent the two premises as true, the conclusion is true as well.

Here is another syllogism that has two possible diagrams for the premises.

Syllogism 2

All humans are primates.
Some humans have tattoos.
Therefore, some things with tattoos are primates.

Let H = the set of humans, P = the set of primates, and T = the set of things with tattoos.

Two possibilities are:

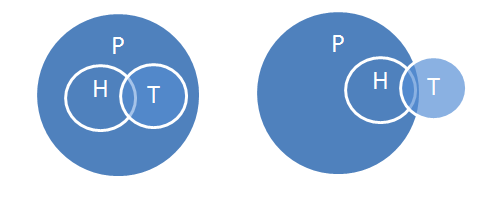
You can see that every way of representing the first two premises of the syllogism as both true has T intersecting H and H contained in P. And you can see that some T must be contained in P, which is what the conclusion asserts.

Here is an example of a syllogism that is not valid, and we can see this even though all the premises and the conclusion are true:

Syllogism 3

All humans are primates.
Some primates are mortal.
Therefore, all humans are mortal.

To see why this is not valid, we can find a way of arranging the circles in a way that the premises are true but the conclusion is false.  The figure below represents a state of affairs that can be imagined in which all humans are primates, some primates are mortal, but all humans are immortal – the opposite of what the conclusion asserts.

 

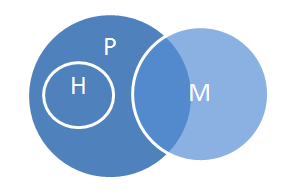
In this invalid syllogism, the truth of the premises does not necessitate the truth of the conclusion.

The validity of a syllogism clearly does not imply that its premises are true or its conclusion is true. The validity of a syllogism doesn’t have anything to do with what the terms of the sentences mean. A valid syllogism could have true premises and a true conclusion or false premises and a true conclusion. But it cannot have true premises and a false conclusion! If the premises are true, the conclusion is necessarily true. This is what is meant by logical arguments being truth preserving.  (For this reason, if you can find an example where the premises are true and the conclusion is false, you can show that a syllogism is invalid – see below.)

Syllogistic Reasoning Rules

The following rules might be helpful in solving syllogism problems:

• From ‘Not all A is B’  infer ‘Some A is not B’, and vice versa.
• From ‘No X are Y’ infer ‘No Y are X’, and vice versa.
• Rule 2:  From ‘All X are Y’ infer ‘Some X are Y’, and vice versa.
• Rule 3: From ‘Some X are Y’ infer ‘Some Y are X’, and vice versa.

Syllogisms involving instances

You can also do syllogistic reasoning where the topic is an individual (e.g. S).

Thus

All men are mortal
Socrates is a man
———————–
Socrates is mortal

Or

What is spiritual is immortal.
The human soul is spiritual.
————————————
The human soul is immortal

Or

Whatever makes unions more democratic is good for unions
The open shop is something that makes unions more democratic
————————————————————————————-
The open shop is good for unions.

 

More Exercises

For more exercises : https://web.cn.edu/kwheeler/documents/Syllogisms.pdf

[space]