Mindware Strategies for How to Represent a Problem When Problem Solving – A Tutorial

The CRT (cognitive reflection test)

The first 3 problems make up what is called the Cognitive Reflection Test (CRT)  It was designed to assesses individuals’ ability to suppress an intuitive and spontaneous (“System 1“) wrong answer in favor of a reflective and deliberative (“System 2“) right answer. In other words the three questions are designed to measure the tendency to override a prepotent response alternative that is incorrect and to engage in further reflection that leads to the correct response.

Research has found that in general

• People with  high CRT scores are patient, allowing for better decisions about good things that could happen in the future, rather than just in the present for immediate gratification.
• People with high CRT scores are not risk-averse for gains and less risk-seeking for losses.

Mindware strategy tip

The first tip is don’t RUSH to a conclusion, and make sure you double check your initial hunch. Slow down. Work through the problem. Check.

Solving these problems can benefit from working them through on paper. The simple act of depicting the problems graphically or in numbers aids System 2 thinking.

• In the lily pad problem, the solution requires working backwards – halving the the number of lilies each step backwards. This can be represented graphically or numerically to get the relevant insight.
• In the widget making problem, you can reason thus: in 1 minute,  1 machine can make 1 widget.  Similarly, in 1 minute, 2 machines could make 2 widgets.   (Or in 2 minutes, 1 machine could make  2 widgets.) So 100 machines would make 100 widgets in 1 minute. (Or in 100 minutes, 1 machine could make 100 widgets.  In 100 minutes, 100 widgets could make 100 x 100 widgets  = 10,000 widgets!)
• In the bat and ball problem, actually do the sums and see if your answer adds up! If you said the ball costs 10 cents, do the sum to check. We know the bat costs $1 more than the ball, so the bat would have to cost $1.10. $1.10 + 0.10 = $1.20.

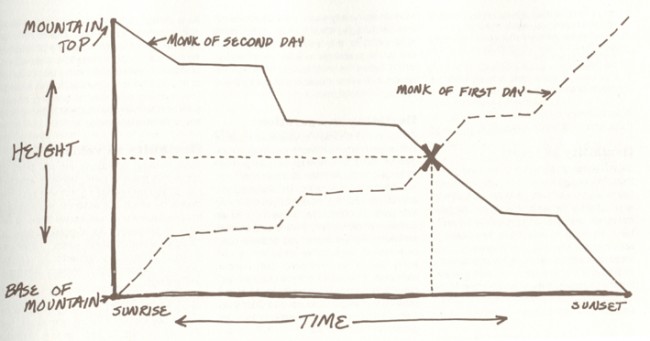
The Buddhist monk problem

Here is one proof. Let ascent and descent be divided between two persons on the same day. They must meet.

Here we can see an obvious proof by represent the problem a little differently (but with the same formal structure).

Here is another way of proving it – using a graphical representation of a proof to this problem: